3名高中生是如何重新证明百年数学定理的？年轻智慧挑战极限

小大

用微信扫描二维码
分享至好友和朋友圈

关键词：

2024-12-02 13:57:31 澎湃新闻

最近，一群高中生在数学领域展现了非凡的才能。量子杂志报道了由Niko Voth、Joshua Broden和Noah Nazareth组成的三人团队，在多伦多大学数学家Malors Espinosa的指导下，证明了一条关于扭结和分形的新定理。

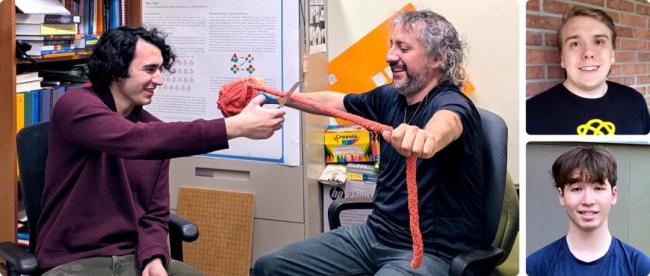
3名高中生是如何重新证明百年数学定理的？

2021年秋天，当时还是多伦多大学数学研究生的Malors开始设计一个特殊的数学问题。多年来，他一直在为当地高中生举办暑期讲习班，教授他们数学研究的基本思想，并展示如何写证明。他希望找到一个适合高中生的问题，既能激发他们的兴趣，又能让他们体验到解决实际问题的过程。

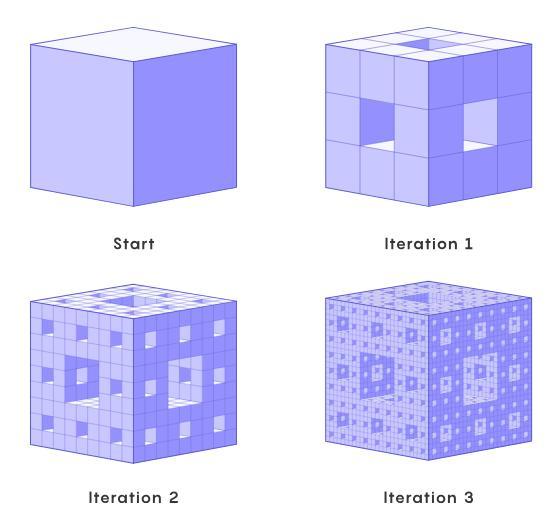
3名高中生是如何重新证明百年数学定理的？年轻智慧挑战极限

Malors在阅读一本关于混沌的教科书时找到了这样的问题。书中提到一种名为门格海绵的分形结构，它通过从立方体中移除越来越小的立方体来构建。自卡尔·门格尔在近一个世纪前提出以来，门格海绵因其独特的性质吸引了许多数学爱好者。经过无数次迭代后，其体积会缩小到零，而表面积则变得无限大。

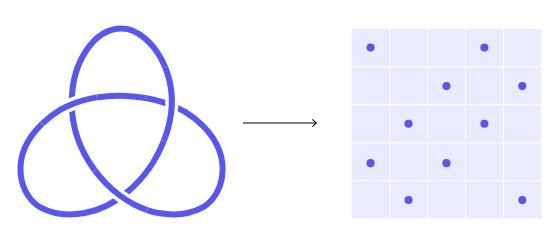
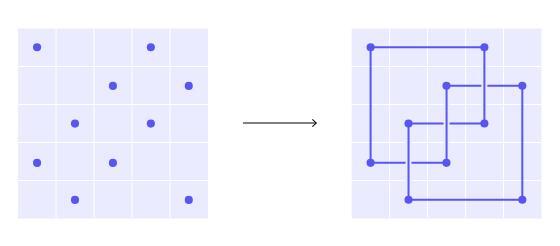
Malors意识到，虽然门格已经证明可以在海绵中找到圆，但并没有证明所有同胚扭结都可以找到。于是，他提出了一个新的问题：是否可以在海绵中找到每个扭结。这个问题激发了年轻学生们的兴趣，他们在Malors的研讨会上学习了扭结理论，并对这个问题产生了浓厚的兴趣。

3名高中生是如何重新证明百年数学定理的？年轻智慧挑战极限

经过几个月与Malors的Zoom会议讨论，三名高中生最终证明了所有扭结确实可以在门格海绵中找到。此外，他们还发现另一种相关的分形也可能存在同样的情况。北卡罗来纳州立大学拓扑学家Radmila Sazdanovic表示，这是一个巧妙的方法，重新审视了一个百年历史的定理，并提出了一个新颖的问题。

3名高中生是如何重新证明百年数学定理的？年轻智慧挑战极限

这些学生不仅解决了Malors的问题，还进一步探索了四面体版本的门格海绵。尽管过程中遇到了一些困难，但他们最终找到了一种新方法，可以将某些类型的扭结嵌入四面体中。这项研究不仅启发了新的艺术成果，还可能提供更广泛适用的测量分形复杂性的方法。

3名高中生是如何重新证明百年数学定理的？年轻智慧挑战极限

目前，这三名学生都已经高中毕业，其中一人决定继续研究四面体问题。他们表示，能够为真理做出贡献是一件非常有意义的事情。这一切都始于问出那个正确的问题。

3名高中生是如何重新证明百年数学定理的？年轻智慧挑战极限

(责任编辑：卢其龙 CN070)

关闭

3名高中生是如何重新证明百年数学定理的？ 年轻智慧挑战极限